Firing Squad Synchronization Problem

New solutions of the 6-states minimal time FSSP

Brief description of the FSSP

The Firing Squad Synchronation Problem (FSSP) is a cellular automata problem which consists of synchronizing all the cells of the automata in the same state (firing state) in minimal time, and for the first time, starting from a cells line in quiecent state (rest state) except one cell on the left in a special state (general state).


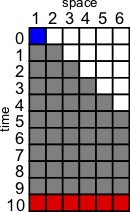
For n=6 cells, the minimal time of synchronization is 2n-2=10 time steps.

The cellular automata is one-dimentional with itself, left- and right-hand neighbors. For the two cells the most left and right on the line, there is only two neighbors (including the cell itself). A cell remains in the quiescent state if all neighbors are in the quiescent state. A solution of the FSSP is a transition rule which synchronizes the cellular automata for any size n greater than 2.
See another description of the problem on wikipedia.

History

The FSSP was proposed by Myhill in 1957 and published by Moore in 1964. The search for optimal time solutions using a minimal number of states is one of the central issues of the research about FSSP. A short history of the solutions found by "hand":

  • 1962, Eiichi Goto, several thousand of states [1],
  • 1966, Abraham Waksman, 16 states [2],
  • 1967, Robert Balzer, 8 states [3],
  • 1986, Jacques Mazoyer, 6 states [5],
  • 1994, Peter Sanders, no solution with 4 states [6].
New solutions found by "computer":
  • 2018, M. Clergue, S. Verel, E. Formenti, 718 new solutions of 6 states [7],
  • 2020, T. T. Nguyen, L. Maignan, Millions of solutions of 6 states [8],


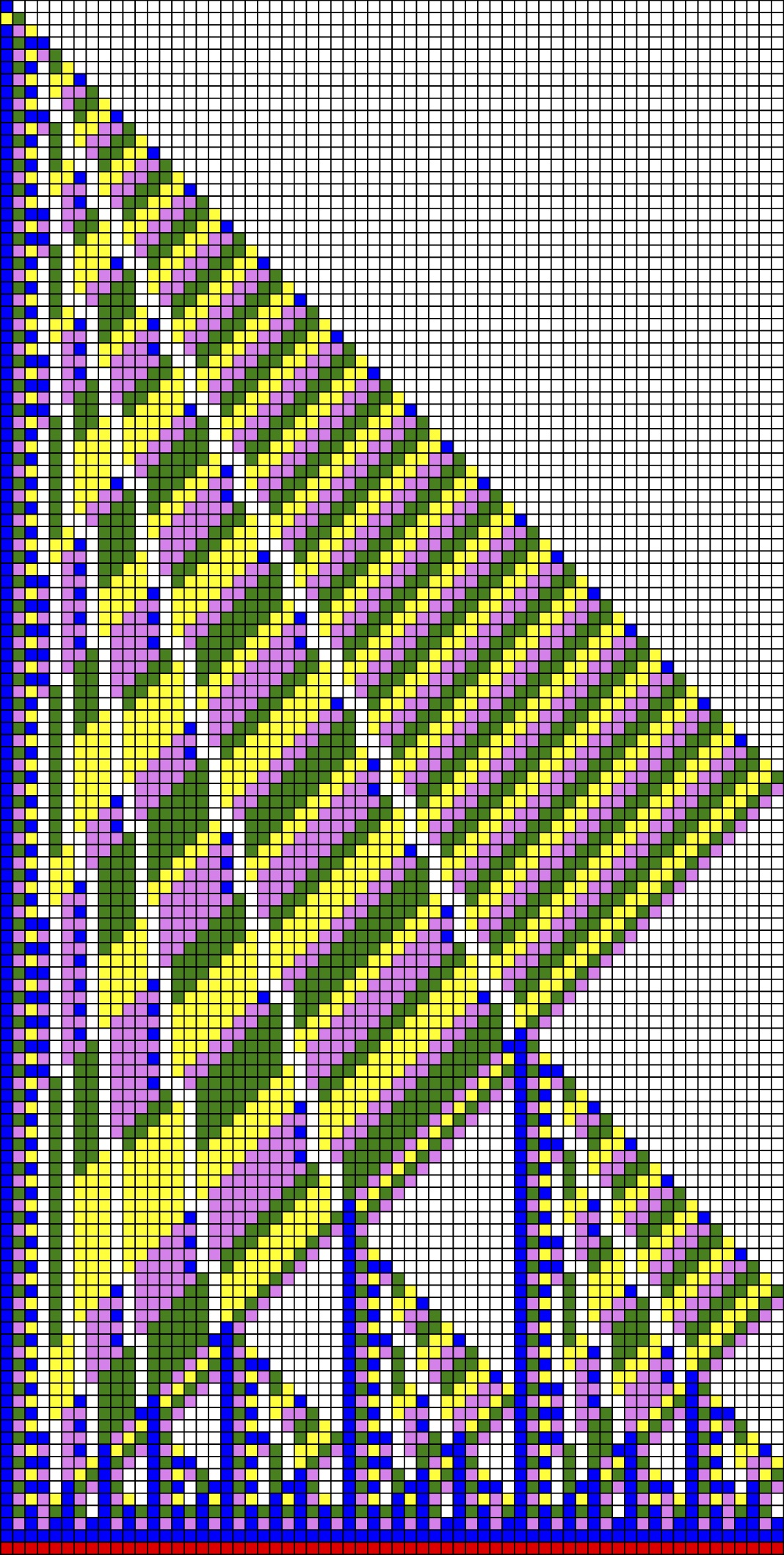
The Jacques Mazoyer solution with 6 states. The only known solution with 6 states until 2018. The Kolmogorov complexity of this solution is 119 which is the number rules used to compute the synchronization.

Bibliography

  1. Eiichi Goto. A minimum time solution of the firing squad problem. Course Notes for Applied Mathematics, 298, 1962.
  2. Abraham Waksman. An optimum solution to the firing squad synchro- nization problem. Information and Control, 9(1):66 – 78, 1966.
  3. Robert Balzer. An 8-state minimal time solution to the firing squad synchronization problem. Information and Control, 10(1):22 – 42, 1967.
  4. Jean-Baptiste Yunes. A propos d’automates cellulaires, suivi par des fonctions booléennes. HDR, 2007
  5. Jacques Mazoyer. A six-state minimal time solution to the firing squad synchronization problem. Theoretical Computer Science, 50(2):183 – 238, 1987.
  6. Peter Sanders. Massively parallel search for transition-tables of polyau- tomata. In W. Wilhelmi C. Jesshope, V. Jossifov, editor, Proc. of the VI Int. Workshop on Parallel Processing by Cellular Automata and Arrays, pages 99–108. Akademie, Berlin, 1994.
  7. Manuel Clergue, Sébastien Verel, Enrico Formenti, An Iterated Local Search to find many solutions of the 6-states Firing Squad Synchronization Problem, Applied Soft Computing, Volume 66, May 2018, Pages 449-461.doi. pdf.
  8. Tien Thao Nguyen, Luidnel Maignan. Exploring Millions of 6-State FSSP Solutions: The Formal Notion of Local CA Simulation, Automata: Cellular Automata and Discrete Complex System, 2020, pages 1-13. doi. pdf.

Overview of new solutions

718 new solutions have been found for FSSP with 6 states in minimal time. For more details, please refer to:
Manuel Clergue, Sébastien Verel, Enrico Formenti, An Iterated Local Search to find many solutions of the 6-states Firing Squad Synchronization Problem, Applied Soft Computing, Volume 66, May 2018, Pages 449-461. doi. pdf.
The following space-time diagrams show some of them. A visualization tool can also be used.

The solution 634 with the lowest Kolmogorov complexity (80):

The solution 3 which is a typical example of the largest cluster of solutions:
The solution 668 is solution with a Mazoyer-like strategy:

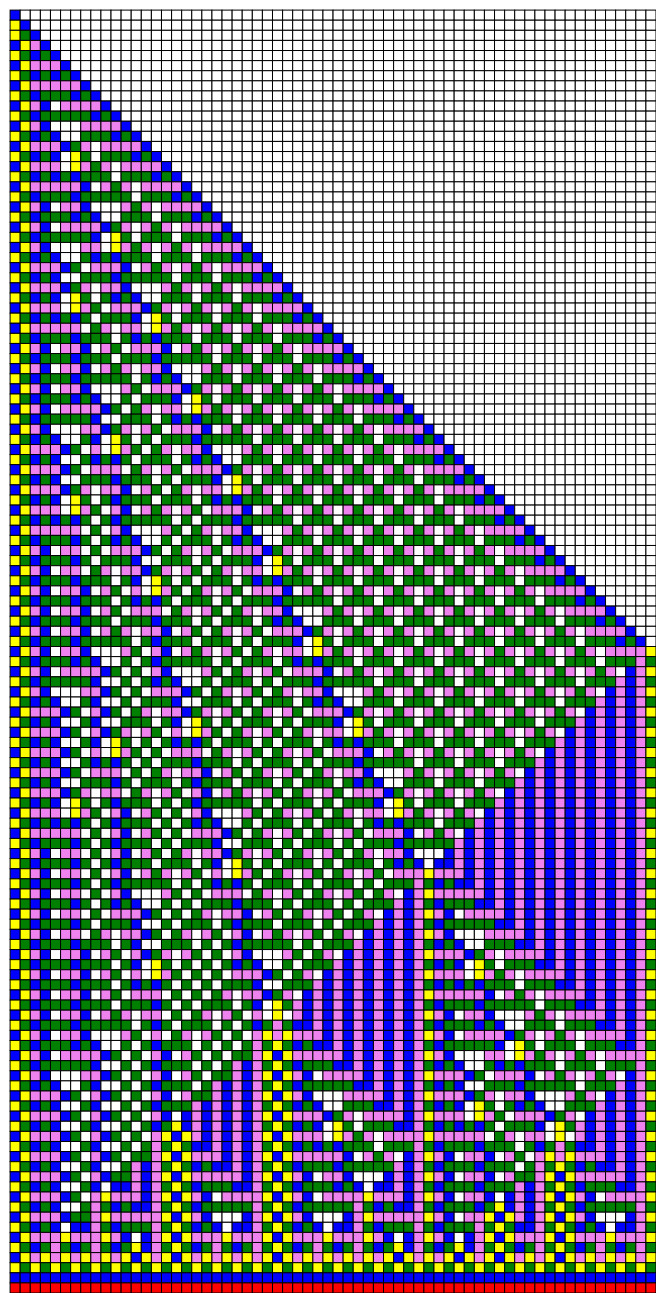
Visualization tool of the new solutions

This tool allows to display the 718 news solutions. The id of the solutions are between 0 and 717. The id 718 is the solution id of the famous Jacques Mazoyer solution.

Solution id:
Line length: between and
Cell size (px):

Your browser does not support the HTML5 canvas tag.

Methodology

To find those new solutions, we model the original problem into an optimization problem, and we use a stochastic local search algorithm (Iterated Local Search) to solve the optimization problem. All details can be found in [7]

Search space

A solution of the FSSP can be encoded by an integer vector. Each integer represents one rule of the cellular automata. There is 172 rules, and the size of the search space is 6^172. But, taking into account some properties of the problem, it is possible to reduce the length of the vector to 165, and the size of the search space to 5^165.

Fitness function

The fitness of a solution (to maximize) is the length of the largest line which is correctly synchronized by the transition rules. For example, the fitness value of rule below is 5 because it is possible to synchronize until the cell line of length 5, but not the length 6 (one cell is in the firing before the minimal time).

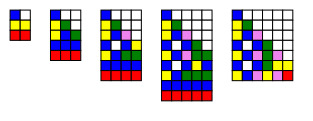
The fitness value of an optimal solution which synchronizes any length greater than 2 is infinite.

Optimization algorithm

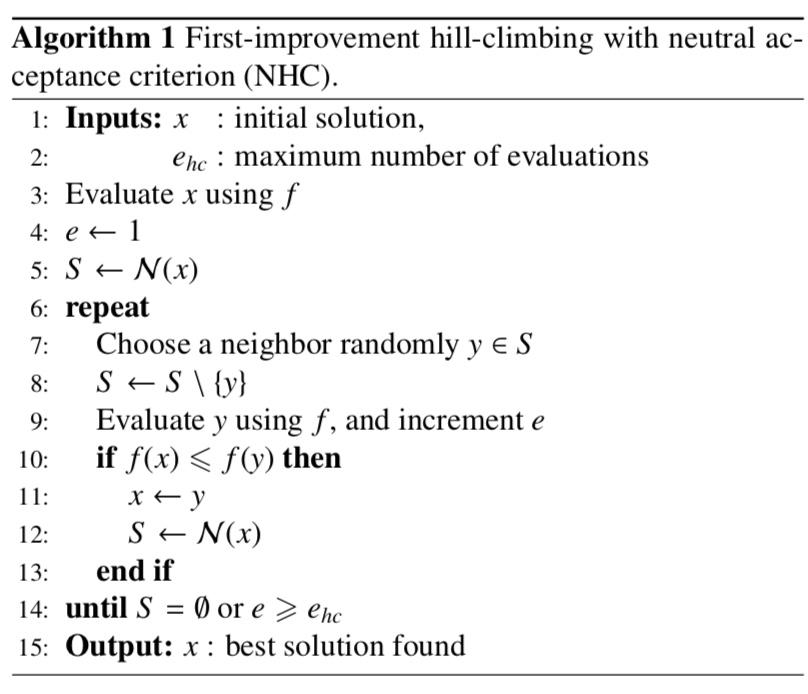
The optimization algorithm is an Iterated Local Search (ILS). Two solutions are neighbors if they differ only by one single rule. The local search is an hill-climbing algorithm with first-improvement acceptance rule, and particular attention on solutions with the same fitness value. The perturbation operator of the ILS modify several (used) rules at random.

Why it works?
On the contrary to a first intuition, the fitness landscape of the FSSP is not completly random, and rugged. Indeed, the fitness landscape is neutral, and the correlation between the fitness of a solution, and the fitness of neighboring solutions is sufficient to ensure the progress of the local search.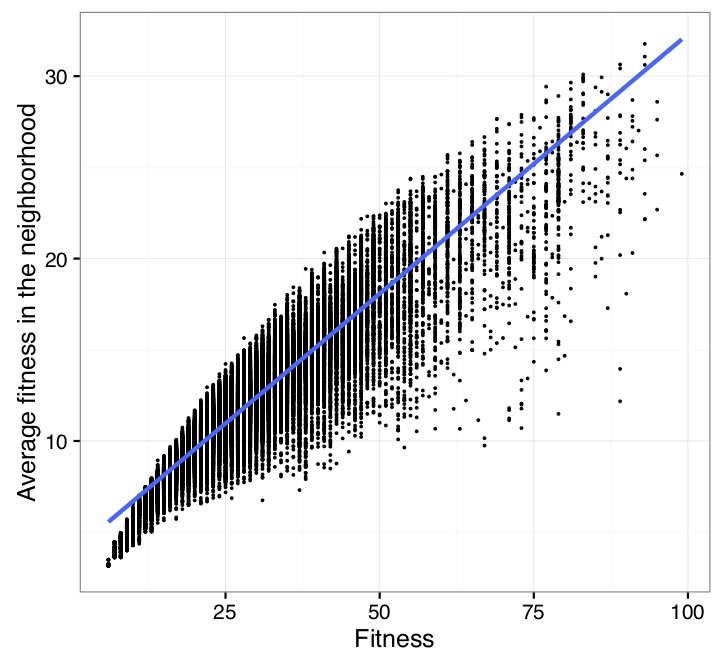

Files with solutions

The rules of the new solutions of the 6-states minimal time FSSP can be found in different formats.
Text format:

All the 718 new solutions can be found in text format within this zip file.
Each solution with the identier id is given in a text file with filename sol_id.cf. Each line of the text file represents one transition rule of the cellular automata. One rule is given by 4 integers: l c r nc. When the state of the left neighbor is l, the state of the cell is c, and the state of the right neighbors is r, then the new state of the cell is nc. The quiescent/rest state is 0, the synchronization/firing state is 5, the active/general state is 1, and the other states are 2, 3, and 4. The number 6 means "border", and is used for the special transition rules of the two left- and right-hand cells of line. For example, 6 1 0 1 means that when the state of the most left cell is 1 and the state on its right neighbor is 0, then the new state is 1.

Pdf format

We also provide a basic pdf file with the rules given by a written tabular: pdf.

If you have any question, please contact the authors: Sébastien Verel (verel@univ-littoral.fr), Manuel Clergue (manuel.clergue@univ-ag.fr), or Enrico Formenti (enrico.formenti@unice.fr).