Neurone de McCulloch et Pitts 

Introduction

Cette applet présente le neurone de McCulloch et Pitts.

Auteurs

Cette applet a été modifiée par Alix Herrmann (EPFL) à partir de l'applet original de Fred Corbett, disponible ici.

Theorie

Le premier modèle computationel de neurone artificiel a été proposé par McCulloch et Pitts en 1943. La principale différence entre ce modèle et le modèle du neurone artificiel est l'utilisation de l'entrée inhibitrice absolue (un 1 sur une entrée inhibitrice désactive le neurone : il produit 0 quelque soient les autres entées).

Les entrées et sorties sont binaires (exclusivement des un ou des zéros) ; les neurones produisent seulement des résultats binaires. Il n'y a pas de poids et la fonction d'activation est toujours la fonction de seuil. Les éléments d'un neurone de McCulloch et Pitts sont donc :

  1. Un ensemble de n entrées excitatrices, xi.
  2. Un ensemble de de m entrées inhibitrices, xn+j
  3. Un seuil, u.
  4. Une fonction d'activation pas unitaire.
  5. Un seul neurone de sortie, y.
Le fonctionnement d'un neurone de McCulloch et Pitts est simple : si au moins une entrée inhibitrice est à 1, la sortie est à 0; sinon, on effectue la somme des entrées excitatrices ; si c'est somme est supérieure ou égale au seuil u, le neurone est actif et sa sortie est à 1; sinon sa sortie est à 0.
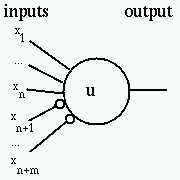
Dans les diagrames, on peut représenter un neurone de McCulloch et Pitts comme un cercle contenant une valeur de seuil ; les entrées inhibitrices sont indiquées par un petit cercle comme ci-dessous :

Applet

  • Pour changer les entrées, cliquez sur les boutons.
  • Pour changer le seuil, tapez une nouvelle valeur dans le champ à l'intérieur du cercle et pressez Entrée.
  • Pour changer le type d'une entrée (inhibtrice en excitatrice et vice versa), cliquez sur la tête de la flèche.

    •  
     

    Questions

    1. Essayez plusieurs configurations (valeur du seuil, entrées excitatrices ou inhibitrices ) du neurone de l'applet, et observez son comportement (sur des configurations différentes en entrée).
    2. Comment, avec un neurone à une entrée, pourrait-on simuler la fonction logique NOT (si l'entrée est 0, la sortie est 1 et si l'entrée est 1, la sortie doit être 0).
    3. Lesquelles des fonction binaires à deux entrées (ET, OU, OU EXCLUSIF,...) peuvent être calculée à l'aide de :