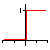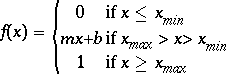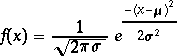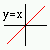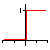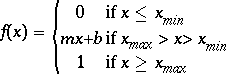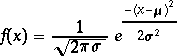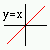Composants d'un neurone artificiel
Entrées, xi:
Typiquement, les valeurs d'entrée sont des stimuli externes en provenance
de l'environnement ou des sorties d'autre neurones artificiels. Elles peuvent
être discrétisées grâce à un ensemble
tel que {0,1} ou bien être des valeurs réelles.
[retour ]
Poids, wi:
La première chose que fait un neurone artificiel est de calculer
la somme pondérée de ses entrées (i.e., le produit
scalaire entre le motif d'entrée et les poids des connexions). Les
poids sont des valeurs réelles qui déterminent la contribution
de chaque entrée.
Le but d'un algorithme d'apprentissage pour un réseau de neurones
est de déterminer le meilleur ensemble de poids pour le problème
en considération. Trouver l'ensemble optimal est souvent un compromis
entre temps de calcul, minimisation de l'erreur et conservation de la capacité
de généralisation pour le réseau.
The goal of neural network training algorithms is to determine the "best"
possible set of weight values for the problem under consideration. Finding
the optimal set is often a trade-off between computation time, minimizing
the network error, and maintaining the network's ability to generalize.
[retour ]
Seuil, u:
Le seuil est un nombre réel qui est soustrait de la somme pondérée
des valeurs d'entrée. Parfois, le seuil est appelé valeur
de biais. Dans ce cas, le nombre réel est aditionné
à la somme des valeurs d'entrée. Pour des raisons de simplicité,
le seuil peut être vu comme une entrée supplémentaire
associée à un poids, où w0
= u et x0 = -1.
[retour ]
Fonction d'activation, f:
La fonction d'activation pour le neurone originel de McCulloch et Pitts
était la fonction pas unitaire. Cependant, le modèle a évolué
et on retrouve maintenant un grand nombre de fonctions d'activation différentes
comme la sigmoïde, linéaire seuillée et gaussienne.
La fonction identité est la plus simple possible ; le résultat
est appelé un associateur linéaire.
Les fonction d'activation disponibles dans cette applet sont illustrées
dans la table 1.
| Pas unitaire |
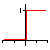 |
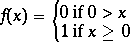 |
| Sigmoïde |
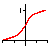 |
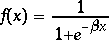 |
| Linéaire Seuillée |
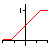 |
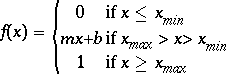 |
| Gaussienne |
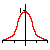 |
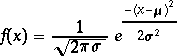 |
|
Identité
|
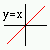 |
f (x) = x |
Table 1: Fonctions d'activation
[retour ]
Sortie du neurone, y:
Le neurone artificiel calcule sa sortie grâce à l'équation
ci-dessous. C'est le résultat correspondant à l'application
de la fonction d'activation à
la somme pondérée des entrées,
moins le seuil. Cette valeur peut être discrète
ou réelle selon la fonction d'activation utilisée.
Une fois que la sortie est calculée, elle peut être passée
à un autre neurone (ou groupe de neurones) ou directement à
l'environnement extérieur. L'interprétation de la sortie
des neurones dépend du problème en considération.
Par exemple, dans la classification de motifs, une sortie de 1 peut signifier
que l'entrée appartient à une certaine classe, alors que
une sortie de 0 signifie le contraire.
[retour ]